รอมบิคิวบอกทาฮีดรอน

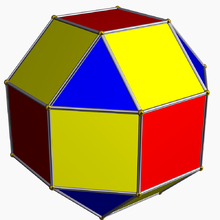
รอมบิคิวบอกทาฮีดรอน

รูปทรงนี้ได้รับการตีพิมพ์เป็นครั้งแรกในหนังสือ Divina Proportione โดยเลโอนาร์โด ดา วินชี

รอมบิคิวบอกทาฮีดรอน (เล็ก) (อังกฤษ: (small) rhombicuboctahedron, พหูพจน์: -dra) เป็นทรงหลายหน้า (polyhedron) ที่ประกอบด้วยหน้ารูปสามเหลี่ยมด้านเท่า 8 หน้า และรูปสี่เหลี่ยมจัตุรัส 18 หน้า รวม 26 หน้า โดยหน้ารูปสามเหลี่ยมทุกหน้าจะมีรูปสี่เหลี่ยมล้อมอยู่โดยรอบ ทรงนี้มี 24 จุดยอด 48 ขอบ และเป็นหนึ่งในทรงตันอาร์คิมิดีส (Archimedean solid)

รูปทรงนี้สามารถเรียกในชื่ออื่นอีกคือ ออร์โทไบคิวโพลาสี่เหลี่ยมจัตุรัสอีลองเกต (elongated square orthobicupola)

พื้นที่ผิวและปริมาตร

รอมบิคิวบอกทาฮีดรอนที่คลี่ออก

พื้นที่ผิว A และปริมาตร V ของรอมบิคิวบอกทาฮีดรอน ที่มีความยาวขอบทุกด้านเท่ากับ a สามารถคำนวณได้ดังนี้

$A=(18+2{\sqrt {3}})a^{2}\approx 21.4641016a^{2}$

$V={\frac {1}{3}}(12+10{\sqrt {2}})a^{3}\approx 8.71404521a^{3}$

พิกัดคาร์ทีเซียน

พิกัดคาร์ทีเซียนของรอมบิคิวบอกทาฮีดรอน สามารถกำหนดพิกัดของจุดยอดได้ดังนี้

(±1, ±1, ±(1+√2))

ดูเพิ่ม

• ทรงลูกบาศก์ (cube)
• คิวบอกทาฮีดรอน (cuboctahedron)
• ทรงแปดหน้า (octahedron)
• รอมบิโคซิโดเดคาฮีดรอน (rhombicosidodecahedron)
• คิวบอกทาฮีดรอนปลายตัด หรือ รอมบิคิวบอกทาฮีดรอนใหญ่ (truncated cuboctahedron หรือ great rhombicuboctahedron)
• ไจโรไบคิวโพลาสี่เหลี่ยมจัตุรัสอีลองเกต (elongated square gyrobicupola)

อ้างอิง

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
• Coxeter, H. S. M. (May 13, 1954). "Uniform Polyhedra". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 246, (916): 401–450.{{cite journal}}: CS1 maint: extra punctuation (ลิงก์)

แหล่งข้อมูลอื่น

• เอริก ดับเบิลยู. ไวส์สไตน์, "Rhombicuboctahedron" จากแมทเวิลด์.
• Archimedes and the Rhombicuboctahedron by Antonio Gutierrez from Geometry Step by Step from the Land of the Incas.
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra