ทรงยี่สิบ-สิบสองหน้าปลายตัด

ทรงยี่สิบ-สิบสองหน้าปลายตัด

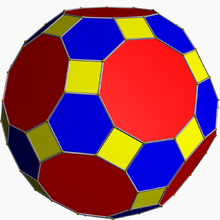
ทรงยี่สิบ-สิบสองหน้าปลายตัด (อังกฤษ: truncated icosidodecahedron) เป็นทรงหลายหน้า (polyhedron) ที่ประกอบด้วยหน้ารูปสี่เหลี่ยมจัตุรัส 30 หน้า หน้ารูปหกเหลี่ยมด้านเท่ามุมเท่า 20 หน้า และหน้ารูปสิบเหลี่ยมด้านเท่ามุมเท่า 12 หน้า รวม 62 หน้า แต่หน้าเรียงตัวโดยไม่มีหน้าชนิดเดียวกันอยู่ติดกัน ทรงนี้มี 120 จุดยอด 180 ขอบ และเป็นทรงตันอาร์คิมิดีส (Archimedean solid)

ชื่ออื่น ๆ

รูปทรงนี้ยังมีชื่อเรียกอื่น ๆ อีกเช่น

• ทรงยี่สิบ-สิบสองหน้าขนมเปียกปูนใหญ่ (great rhombicosidodecahedron)
• รอมบิทรันเคตทรงยี่สิบ-สิบสองหน้า (rhombitruncated icosidodecahedron)
• ออมนิทรันเคตทรงยี่สิบ-สิบสองหน้า (omnitruncated icosidodecahedron)

สำหรับชื่อ ทรงยี่สิบ-สิบสองหน้าปลายตัด ได้การตั้งขึ้นโดย โยฮันน์ เคปเลอร์ (Johannes Kepler) ซึ่งเป็นการเข้าใจผิด เนื่องจากถ้านำเอาทรงยี่สิบ-สิบสองหน้า (icosidodecahedron) มาตัดปลายจริง ๆ จะได้ส่วนที่ตัดเป็นหน้ารูปสี่เหลี่ยมผืนผ้าทองคำไม่ใช่จัตุรัส

ส่วนชื่อ ทรงยี่สิบ-สิบสองหน้าขนมเปียกปูนใหญ่ อาจจะทำให้สับสนกับอีกรูปทรงหนึ่งที่มีชื่อเดียวกันคือ ทรงยี่สิบ-สิบสองหน้าขนมเปียกปูนใหญ่เอกรูป (uniform great rhombicosidodecahedron) ซึ่งไม่ใช่ทรงหลายหน้าแบบนูน (nonconvex)

พื้นที่ผิวและปริมาตร

ทรงยี่สิบ-สิบสองหน้าปลายตัดที่คลี่ออก

พื้นที่ผิว A และปริมาตร V ของทรงยี่สิบ-สิบสองหน้าปลายตัด ที่มีความยาวขอบทุกด้านเท่ากับ a สามารถคำนวณได้ดังนี้

${\begin{aligned}A&=30\left[1+{\sqrt {2\left(4+{\sqrt {5}}+{\sqrt {15+6{\sqrt {6}}}}\right)}}\right]a^{2}\\&\approx 175.031045a^{2}\\V&=(95+50{\sqrt {5}})a^{3}\approx 206.803399a^{3}\\\end{aligned}}$

พิกัดคาร์ทีเซียน

พิกัดคาร์ทีเซียนของจุดยอดของทรงยี่สิบ-สิบสองหน้าปลายตัด สามารถกำหนดพิกัดได้ดังนี้

(±1/τ, ±1/τ, ± (3+τ))

(±2/τ, ±τ, ± (1+2τ))

(±1/τ, ±τ², ± (-1+3τ))

(± (-1+2τ) , ±2, ± (2+τ))

(±τ, ±3, ±2τ)

เมื่อ τ = (1+√5) /2 หรืออัตราส่วนทอง

อ้างอิง

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)

ดูเพิ่ม

• ทรงสิบสองหน้า (dodecahedron)
• ทรงยี่สิบหน้า (icosahedron)
• ทรงยี่สิบ-สิบสองหน้า (icosidodecahedron)
• คิวบอกทาฮีดรอนปลายตัด (truncated cuboctahedron)

แหล่งข้อมูลอื่น

• เอริก ดับเบิลยู. ไวส์สไตน์, "GreatRhombicosidodecahedron" จากแมทเวิลด์.
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra