การแจกแจงแบบปรกติ

Probability density function The red line is the standard normal distribution
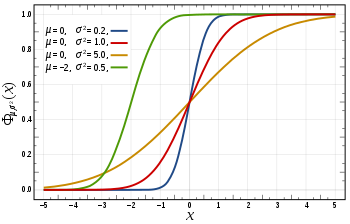Cumulative distribution function Colors match the image above
notation:	$\mathcal{N}(\mu,\,\sigma^2)$
parameters:	μ ∈ R — mean (location) σ2 > 0 — variance (squared scale)
support:	x ∈ R
pdf:	$\tfrac{1}{\sqrt{2\pi\sigma^2}}\,e^{ -\frac{(x-\mu)^2}{2\sigma^2} }$
cdf:	$\frac12\Big[1 + \operatorname{erf}\Big( \frac{x-\mu}{\sqrt{2\sigma^2}}\Big)\Big]$
mean:	μ
median:	μ
mode:	μ
variance:	σ2
skewness:	0
ex.kurtosis:	0
entropy:	$\tfrac12 \ln(2 \pi e \, \sigma^2)$
mgf:	$\exp\{ \mu t + \tfrac{1}{2}\sigma^2t^2 \}$
cf:	$\exp \{ i\mu t - \tfrac{1}{2}\sigma^2 t^2 \}$
Fisher information:	$\begin{pmatrix}1/\sigma^2&0\\0&1/(2\sigma^4)\end{pmatrix}$

สำหรับทฤษฎีความน่าจะเป็น การแจกแจงแบบปรกติ (อังกฤษ: Normal Distribution) เป็นการแจกแจงความน่าจะเป็นของค่าของตัวแปรสุ่มที่เป็นค่าแบบต่อเนื่อง โดยที่ค่าของตัวแปรสุ่มมีแนวโน้มที่จะมีค่าอยู่ใกล้ๆกับค่าๆหนึ่ง (เรียกว่าค่ามัชฌิม) กราฟแสดงค่าฟังก์ชันความหนาแน่น (probability density function) จะเป็นรูปคล้ายระฆังคว่ำ หรือเรียกว่า Guassian function โดยค่าฟังก์ชันความหนาแน่นของการแจกแจงแบบปรกติ ได้แก่

$f(x) = \tfrac{1}{\sqrt{2\pi\sigma^2}}\; e^{ -\frac{(x-\mu)^2}{2\sigma^2} },$

โดย "x" แทนตัวแปรสุ่ม พารามิเตอร์ μ แสดงค่ามัชฌิม และ σ² คือค่าความแปรปรวน (variance) ซึ่งเป็นค่าที่ใช้บอกปริมาณการกระจายของการแจกแจง การแจกแจงแบบปรกติที่มีค่า μ = 0 และ σ² = 1 จะถูกเรียกว่า การแจกแจงแบบปรกติมาตราฐาน

การแจกแจงแบบปรกติเป็นการแจกแจงที่เด่นที่สุดในทางวิชาความน่าจะเป็นและสถิติศาสตร์ ซึ่งก็มาจากหลายๆเหตุผล ซึ่งก็รวมถึงผลจาก Central Limit Theorem ที่กล่าวว่า ภายใต้สภาพทั่วๆไปแล้ว ค่าเฉลี่ยจากการสุ่มค่าของตัวแปรสุ่มอิสระจากการแจกแจงใดๆ (ที่มีค่าเฉลี่ยและค่าความแปรปรวนจำกัด) ถ้าจำนวนการสุ่มนั้นใหญ่พอ แล้วค่าเฉลี่ยนั้นจะมีการแจกแจงประมาณได้เป็นการแจกแจงแบบปรกติ

บทความที่เกี่ยวข้อง

• การแจกแจงแบบปรกติหลายตัวแปร