การวางแผนการเคลื่อนที่

การวางแผนการเคลื่อนที่ (อังกฤษ: motion planning) เป็นคำที่ใช้ในวิทยาการหุ่นยนต์ โดยมีความสำคัญต่อการพัฒนาหุ่นยนต์อัตโนมัติเป็นอย่างมาก ตัวอย่างของการวางแผนการเคลื่อนที่ได้แก่ ในกรณีของหุ่นยนต์เคลื่อนที่ได้ (mobile robot) เมื่อได้รับคำสั่งให้เดินทางจากห้องหนึ่งไปยังห้องถัดไปในอาคารสำนักงาน หุ่นยนต์จะมีวิธีการเดินทางอย่างไรเพื่อไปถึงจุดหมายโดยไม่ชนกับสิ่งกีดขวาง และไม่ตกบันได เป็นต้น ในกรณีของแขนกล (robot arm) ที่ใช้ในอุตสาหกรรม การวางแผนการเคลื่อนที่อาจสนใจว่าแต่ละข้อต่อ (joint) จะเคลื่อนไหวอย่างไรเพื่อไปหยิบจับวัตถุ และในกรณีของหุ่นยนต์ฮิวแมนนอยด์ หุ่นยนต์จะทำอย่างไรเพื่อก้มเก็บของที่อยู่ใต้โต๊ะ หรือจะก้าวเดินอย่างไร (footstep planning^[1]) โดยไม่ให้เหยียบสิ่งกีดขวางที่พื้น เป็นต้น

หลักการ[แก้]

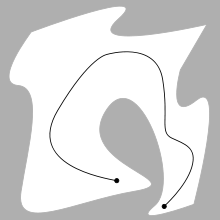
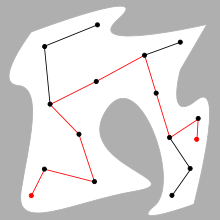
ปัญหาพื้นฐานของการวางแผนการเคลื่อนที่คือการสร้างการเคลื่อนไหวอย่างต่อเนื่องตั้งแต่จุดเริ่มต้นไปยังจุดเป้าหมายโดยไม่ชนสิ่งกีดขวาง (obstacle) โดย ณ ตำแหน่งเริ่มต้น ท่าทางหรือโครงแบบ (configuration) ของหุ่นยนต์มักเขียนแทนด้วย S (starting configuration) ในขณะที่โครงแบบเป้าหมายนั้นแทนด้วย G (goal configuration) ปัญหาการวางแผนการเคลื่อนที่ของหุ่นยนต์ที่ง่ายที่สุด คือกรณีทราบตำแหน่งของสิ่งกีดขวางอยู่แต่แรก โดยปกติ เรขาคณิตของหุ่นยนต์และสิ่งกีดขวางอยู่ในปริภูมิ 2 มิติ หรือ 3 มิติ ที่เราเรียกว่า พื้นที่งาน (workspace) อย่างไรก็ตามเส้นทาง (path) การเคลื่อนที่ของหุ่นยนต์จะถูกอธิบายในปริภูมิโครงแบบ (configuration space) ซึ่งโดยปกติเป็นปริภูมิสูง

ปริภูมิโครงแบบ[แก้]

ท่าทางหนึ่งๆ (pose) ของหุ่นยนต์ถูกเรียกว่าเป็น "โครงแบบ" (configuration) ของหุ่นยนต์ เซ็ตของโครงแบบที่เป็นไปได้ทั้งหมดเรียกว่า ปริภูมิโครงแบบ (configuration space) และมักนิยมเขียนแทนด้วยเซต C ยกตัวอย่างเช่น

สมมติหุ่นยนต์มีขนาดเป็นเพียงจุด (ไม่มีขนาด) เคลื่อนที่บนพื้นที่งานที่เป็นระนาบ 2 มิติ ในกรณีนี้ปริภูมิโครงแบบ C คือระนาบ และโครงแบบของหุ่นยนต์สามารถเขียนอธิบายได้ด้วยพารามิเตอร์ 2 ค่าคือ (x, y)
ถ้าหุ่นยนต์มีรูปร่างเพียง 2 มิติที่สามารถเลื่อนตำแหน่งและหมุนได้ พื้นที่งานในกรณีนี้จะยังคงเป็น 2 มิติ แต่ปริภูมิโครงแบบ C จะเป็นยูคลิเดียนกรุปแบบพิเศษ (special Euclidean group) SE(2) = R² $\times$ SO(2) (โดยที่ SO(2) เป็น special orthogonal group ของการหมุนใน 2 มิติ) และโครงแบบในกรณีนี้สามารถอธิบายได้ด้วยพารามิเตอร์ 3 ค่า ได้แก่ (x, y, θ)
ถ้าหุ่นยนต์มีรูปร่างเพียง 2 มิติที่สามารถเลื่อนตำแหน่งและหมุนได้ พื้นที่งานในกรณีนี้จะเป็น 3 มิติ แต่ปริภูมิโครงแบบ C จะเป็นยูคลิเดียนกรุปแบบพิเศษ (special Euclidean group) SE(3) = R³ $\times$ SO(3) และโครงแบบในกรณีนี้สามารถอธิบายได้ด้วยพารามิเตอร์ 6 ค่า ได้แก่ (x, y, z) สำหรับการเลื่อนตำแหน่ง และ มุมออยเลอร์ (Euler_angles) (α, β, γ)
ถ้าหุ่นยนต์เป็นหุ่นยนต์แบบแขนกลยึดติดอยู่กับที่ และมีข้อต่อจำนวน N ปริภูมิโครงแบบ C ในกรณีนี้จะเป็นปริภูมิ N มิติ

ปริภูมิว่าง[แก้]

เซตของปริภูมิโครงแบบที่ไม่เกิดการชนกันกับสิ่งกีดขวาง เรียกว่า ปริภูมิว่าง (free space) เขียนแทนด้วย C_free ส่วนเติมเต็มของ C_free ในปริภูมิโครงแบบ C เรียกว่า obstacle region หรือ forbidden region เขียนแทนด้วย C_obs

โดยปกติการคำนวณหา C_free อยู่ตรงไหนในพื้นที่งานบ้างทำได้ยากมาก อย่างไรก็ตามปัจจุบันนี้การทดสอบว่าโครงแบบของหุ่นยนต์อยู่ใน C_free หรือไม่ สามารถทำได้โดยค่อนข้างมีประสิทธิภาพ กล่าวคือเริ่มต้นจากการใช้ forward kinematics เพื่อหาตำแหน่งทางเรขาคณิตของหุ่นยนต์ จากนั้นใช้การทดสอบการชนกัน (collision detection) เพื่อทดสอบว่าหุ่นยนต์ชนกับสิ่งกีดขวางหรือไม่

ขั้นตอนวิธี[แก้]

Grid-Based Search
Geometric Algorithms
- Visibility Graph
- Cell Decomposition
Potential Fields
Sampling-Based Algorithms
- Probabilistic Roadmap (PRM)^[2]
- Lazy PRM^[3]
- Rapidly-exploring random tree (RRT)^[4]

การประยุกต์ใช้งาน[แก้]

การเคลื่อนที่ของหุ่นยนต์ (Robot navigation)
ระบบอัตโนมัติ (Automation)
รถไร้คนขับ (Driverless car)
หุ่นยนต์ศัลยกรรม (Robotic surgery)
แอนิเมชัน
protein folding

ดูเพิ่ม[แก้]

kinodynamic planning

อ้างอิง[แก้]

↑ Kuffner, J. and Nishiwaki, K. and Kagami, S. and Inaba, M. and Inoue, H. (2001), "Footstep planning among obstacles for biped robots" (PDF), Proc. of 2001 IEEE Intl. Conf. on Intelligent Robots and Systems (IROS 2001){{citation}}: CS1 maint: multiple names: authors list (ลิงก์)
↑ Kavraki, L. E.; Svestka, P.; Latombe, J.-C.; Overmars, M. H. (1996), "Probabilistic roadmaps for path planning in high-dimensional configuration spaces", IEEE Transactions on Robotics and Automation, 12 (4): 566–580, doi:10.1109/70.508439.
↑ Bohlin, R. and Kavraki, LE (2000), "Path planning using lazy PRM" (PDF), IEEE International Conference on Robotics and Automation, 2000. Proceedings. ICRA'00{{citation}}: CS1 maint: multiple names: authors list (ลิงก์)^{[ลิงก์เสีย]}
↑ Lavalle, S.M. (1998). "Rapidly-exploring random trees: A new tool for path planning". Computer Science Dept, Iowa State University, Tech. Rep. TR: 98–11. สืบค้นเมื่อ 2008-06-30.

แหล่งข้อมูลอื่น[แก้]

Robot Motion Planning โดย Jean-Claude Latombe สำนักพิมพ์ Kluwer Academic Publishers
Planning Algorithms โดย Steven M. LaValle สำนักพิมพ์ Cambridge University Press (ISBN 0-521-86205-1)
Principles of Robot Motion: Theory, Algorithms, and Implementation โดย H. Choset, W. Burgard, S. Hutchinson, G. Kantor, L. E. Kavraki, K. Lynch, และ S. Thrun สำนักพิมพ์ MIT Press จัดพิมพ์เมื่อ เมษายน ค.ศ. 2005

บทความเทคโนโลยี หรือ สิ่งประดิษฐ์นี้ยังเป็นโครง คุณสามารถช่วยวิกิพีเดียได้โดยการเพิ่มเติมข้อมูล

[kuffner2001footstep-1] Kuffner, J. and Nishiwaki, K. and Kagami, S. and Inaba, M. and Inoue, H. (2001), "Footstep planning among obstacles for biped robots" (PDF), Proc. of 2001 IEEE Intl. Conf. on Intelligent Robots and Systems (IROS 2001){{citation}}: CS1 maint: multiple names: authors list (ลิงก์)

[2] Kavraki, L. E.; Svestka, P.; Latombe, J.-C.; Overmars, M. H. (1996), "Probabilistic roadmaps for path planning in high-dimensional configuration spaces", IEEE Transactions on Robotics and Automation, 12 (4): 566–580, doi:10.1109/70.508439.

[bohlin2000path-3] Bohlin, R. and Kavraki, LE (2000), "Path planning using lazy PRM" (PDF), IEEE International Conference on Robotics and Automation, 2000. Proceedings. ICRA'00{{citation}}: CS1 maint: multiple names: authors list (ลิงก์)^{[ลิงก์เสีย]}

[Lavalle1998-4] Lavalle, S.M. (1998). "Rapidly-exploring random trees: A new tool for path planning". Computer Science Dept, Iowa State University, Tech. Rep. TR: 98–11. สืบค้นเมื่อ 2008-06-30.

[1]

[2]

[3]

[4]